카이사르 암호
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
1. 개요
카이사르 암호는 율리우스 카이사르가 군사적 메시지를 보호하기 위해 사용한 단순한 치환 암호의 일종이다. 알파벳 문자를 일정 간격으로 밀어내는 방식으로 암호화되며, 무차별 대입 공격이나 빈도 분석과 같은 간단한 방법으로 해독될 수 있다. 고대 로마 시대부터 중세 시대를 거쳐 현대까지 다양한 형태로 활용되었으며, ROT13과 같은 변형도 존재한다. 그러나 보안성은 매우 낮아 현대 암호학에서는 거의 사용되지 않는다.
더 읽어볼만한 페이지
- 고전 암호 - 치환 암호
치환 암호는 평문의 글자를 다른 글자나 기호로 대체하는 암호화 방식으로, 고대부터 사용되었으며 명칭 암호와 동음이의 암호 등의 형태로 발전해 왔고, 현대에는 스포일러 방지 용도로 사용되기도 한다. - 고전 암호 - M-94
M-94는 제2차 세계 대전 초기에 미국에서 사용된 수동 암호 장치로, 25개의 알파벳 원반이 부착된 막대 형태로 메시지를 암호화하고 해독하는 데 사용되었으나, 후에 운용상 허점과 암호 분석 기술 발전으로 기계식 로터 머신으로 대체되었다. - 율리우스 카이사르 - 율리우스력
율리우스력은 율리우스 카이사르가 제정한 역법으로, 365일의 평년과 366일의 윤년으로 구성되며, 태양년과의 오차로 인해 그레고리력으로 대체되었으나, 현재는 일부 지역에서 사용된다. - 율리우스 카이사르 - 갈리아 전쟁
갈리아 전쟁은 카이사르의 정치적 야망, 갈리아의 불안정, 게르만족 침입이 맞물려 기원전 58년부터 50년까지 벌어진 로마의 갈리아 정복 전쟁으로, 카이사르의 권력 강화와 로마 공화정 몰락의 전환점이 되었으나 기록의 신뢰성 및 잔혹성 비판도 존재한다. - 군론 - 점군
점군은 도형의 병진 조작을 제외한 대칭 조작들의 집합으로 군론의 공리를 만족하며, 쉐인플리스 기호나 허먼-모건 기호로 표기되고, 대칭 조작에 대응하는 행렬 표현은 가약 표현과 기약 표현으로 분해될 수 있다. - 군론 - 파울리 행렬
파울리 행렬은 양자역학에서 스핀을 나타내는 데 사용되는 에르미트 행렬이자 유니타리 행렬로, 행렬식은 -1이고 대각합은 0이며, 리 대수의 생성원이자 파울리 벡터로 정의되어 다양한 물리학 분야에서 활용된다.
| 카이사르 암호 | |
|---|---|
| 개요 | |
| 유형 | 환자 암호 |
| 암호 강도 | 매우 약함 |
| 키 | 1~25 |
| 역사 | |
| 고안자 | 가이우스 율리우스 카이사르 |
| 사용 시기 | 기원전 100년 ~ 기원전 44년 |
| 암호화 | |
| 예시 | 평문: "AVVV AVVV AVVV" 암호문: "EXYY EXYY EXYY" |
| 설명 | 각 글자를 오른쪽으로 3만큼 이동시킨 것이다. A는 D가 되고, V는 Y가 된다. |
| 암호화 방법 | 각 글자를 키 값만큼 이동시킨다. |
| 복호화 방법 | 각 글자를 키 값만큼 반대 방향으로 이동시킨다. |
| 기타 | |
| 다른 이름 | 이동 암호 카이사르 시프트 시프트 암호 |
| 관련 암호 | 비즈네르 암호 |
2. 역사

카이사르 암호는 고대 로마 시대부터 사용되어 온 암호화 방식으로, 현대에도 그 흔적을 찾아볼 수 있다.
카이사르 암호는 비밀 해독 반지와 같은 어린이 장난감에서 찾아볼 수 있으며, ROT13 알고리즘으로 Usenet에서 텍스트를 난독화하는 데 사용되기도 한다.[13]
비제네르 암호는 각 위치에서 서로 다른 시프트를 사용하여 카이사르 암호를 활용한다. 시프트 값은 반복되는 키워드로 정의되는데,[14] 키워드가 메시지와 길이가 같고 무작위로 선택되며 다른 사람에게 알려지지 않고 재사용되지 않으면 일회용 패드 암호가 되어 풀 수 없다. 그러나 이러한 조건은 실제로 사용하기 어렵다. 메시지보다 짧은 키워드는 빈도 분석으로 감지될 수 있는 주기적 패턴을 만들기 때문이다.[15]
2006년 4월, 시칠리아 마피아 보스 베르나르도 프로벤자노는 카이사르 암호의 변형을 사용하다 체포되었다. 그의 암호는 숫자를 사용하여 "A"를 "4", "B"를 "5" 등으로 표현했다.[16]
2011년, 라지브 카림은 영국항공 비행기 폭파 등을 논의하며 방글라데시 이슬람 활동가들과 카이사르 암호를 사용하여 통신한 혐의로 유죄 판결을 받았다. 이들은 더 나은 암호화 기술 대신 자신들만의 방식을 사용했는데, 이는 비신자들이 알면 덜 안전하다고 생각했기 때문이다.[17]
2. 1. 고대 로마 시대
율리우스 카이사르는 군사적으로 중요한 메시지를 보호하기 위해 세 글자씩 이동하는 방식(암호화할 때 A는 D가 되고, 해독할 때 D는 A가 되는 방식)을 사용했다.[4] 수에토니우스는 카이사르가 이 방식을 처음 사용한 것으로 기록했지만, 다른 치환 암호는 이보다 먼저 사용된 것으로 알려져 있다.[5][6]수에토니우스의 ''율리우스 카이사르 전기'' 56에 따르면, 카이사르는 기밀 유지가 필요한 경우 알파벳 순서를 바꾸는 방식으로 암호를 사용했다. 해독을 위해서는 A 대신 D를 사용하는 것처럼, 알파벳의 네 번째 문자를 원래 문자 대신 사용해야 했다.[32]
카이사르의 조카인 아우구스투스도 암호를 사용했지만, 한 글자씩 오른쪽으로 이동하고 알파벳의 처음으로 되돌아가지 않는 방식을 사용했다. 수에토니우스의 ''아우구스투스 전기'' 88에 따르면, 아우구스투스는 암호로 글을 쓸 때 A 대신 B, B 대신 C를 쓰는 방식으로 Z 대신 AA를 사용했다.[33]
아울루스 겔리우스는 카이사르의 암호에 관한 논문을 언급하며, 카이사르가 더 복잡한 시스템을 사용했을 수도 있다는 증거를 제시한다.[7][34]
카이사르 암호가 당시 얼마나 효과적이었는지는 알려져 있지 않다. 간단한 치환 암호를 풀기 위한 기술에 대한 기록은 당시 존재하지 않았으며, 가장 오래된 기록은 9세기 알킨디의 빈도 분석 발견과 함께 아랍 세계에서 시작된다.[8][36]
2. 2. 중세 및 근대
유대교 메주자 두루마리 뒷면에서는 히브리어 버전의 카이사르 암호로 암호화된 텍스트 조각이 발견되기도 했다. 각 문자를 히브리 알파벳에서 그 앞의 문자로 대체하면, 이 텍스트는 "YHWH, 우리 하나님, YHWH"로 번역되며, 이는 두루마리의 주요 부분에서 인용한 것이다.[9][10]19세기 신문의 개인 광고 섹션에서는 간단한 암호 방식을 사용하여 암호화된 메시지를 교환하기도 했다. 데이비드 칸(1967)은 ''더 타임스''에서 카이사르 암호를 사용하여 비밀 통신을 하는 연인들의 사례를 묘사했다.[11] 1915년, 러시아군은 군대가 익히기 어려운 복잡한 암호를 대체하기 위해 카이사르 암호를 사용했다. 독일과 오스트리아의 암호 해독가들은 러시아군의 메시지를 해독하는 데 큰 어려움을 겪지 않았다.[12]
3. 암호화 및 복호화 원리
카이사르 암호는 알파벳을 특정 거리만큼 이동시켜 암호화 및 복호화를 수행한다. 예를 들어, 키가 3인 경우, 평문의 각 문자를 알파벳 순서상 세 칸 뒤의 문자로 바꾸어 암호문을 만든다. (A는 D로, B는 E로, ..., Z는 C로).[46]
| 평문 | A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 암호문 (3칸 이동) | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z | A | B | C |
암호화 예시:
- 평문: THE QUICK BROWN FOX JUMPS OVER THE LAZY DOG
- 암호문: QEB NRFZH YOLTK CLU GRJMP LSBO QEB IXWV ALD
복호화는 암호화의 반대 과정으로, 암호문의 각 문자를 알파벳 순서상 세 칸 앞의 문자로 바꾸어 평문을 얻는다. (D는 A로, E는 B로, ..., C는 Z로).
이러한 과정은 모듈러 산술을 사용하여 수학적으로 표현할 수 있다. A=0, B=1, ..., Z=25와 같이 알파벳을 숫자로 변환하면, 문자 x를 n칸 이동시키는 암호화() 및 복호화()는 다음과 같이 나타낼 수 있다.[45]
:
:
(여기서 "mod"는 모듈로 연산을 의미한다. x는 0부터 25 사이의 값을 가지며, 만약 x + n 또는 x - n의 결과가 이 범위를 벗어나면 26을 더하거나 뺀다.)
카이사르 암호는 메시지 전체에 걸쳐 동일한 방식으로 문자를 교환하므로 단일 치환 암호에 속한다.
3. 1. 암호화
카이사르 암호에서 암호화는 평문을 암호문으로 바꾸는 과정이다. 이 과정은 두 가지 방법으로 설명할 수 있다.첫 번째 방법은 알파벳을 특정 칸만큼 이동시키는 것이다. 예를 들어, 아래 표는 알파벳을 왼쪽으로 3칸 이동시킨(오른쪽으로 23칸 이동시킨 것과 동일) 암호화 방식을 보여준다. 이때 이동 칸 수는 키가 된다.
| 평문 | A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 암호문 | X | Y | Z | A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W |
위 표를 사용하여 "THE QUICK BROWN FOX JUMPS OVER THE LAZY DOG"라는 평문을 암호화하면 "QEB NRFZH YOLTK CLU GRJMP LSBO QEB IXWV ALD"가 된다. 복호화는 이 과정을 반대로 수행하여, 암호문을 오른쪽으로 3칸 이동시키면 된다.
두 번째 방법은 모듈러 산술을 사용하는 것이다. 먼저 A를 0, B를 1, ..., Z를 25와 같이 각 알파벳을 숫자로 바꾼다.[2] 그런 다음, 문자 ''x''를 ''n''칸 이동시켜 암호화하는 것을 다음 수학 공식으로 나타낼 수 있다.[3]
:
복호화는 다음과 같이 표현된다.
:
여기서 "mod"는 모듈로 연산을 의미한다. ''x'' 값은 0에서 25 사이여야 하지만, ''x'' + ''n'' 또는 ''x'' - ''n''이 이 범위를 벗어나면 26을 더하거나 빼서 조정해야 한다.
카이사르 암호는 메시지 전체에서 동일한 변환 방식을 사용하기 때문에 단일 문자 치환 암호의 일종으로, 다중 문자 치환 암호와는 다르다.
3. 2. 복호화
카이사르 암호에서 복호화는 암호화의 역과정으로, 암호문을 평문으로 변환하는 과정이다. 이 과정은 암호화에 사용된 키, 즉 알파벳을 이동시킨 횟수만큼 반대 방향으로 이동시켜 수행한다. 예를 들어, 왼쪽으로 3칸 이동하는 키를 사용한 암호문의 경우, 복호화는 오른쪽으로 3칸 이동시켜 수행한다.아래 표는 왼쪽으로 3칸 이동하는 카이사르 암호의 복호화 과정을 보여준다.
| 암호문 | A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 평문 | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z | A | B | C |
예시:
- 암호문: QEB NRFZH YOLTK CLU GRJMP LSBO QEB IXWV ALD
- 평문: THE QUICK BROWN FOX JUMPS OVER THE LAZY DOG
복호화는 모듈러 산술을 사용하여 수학적으로 표현할 수도 있다. 문자 ''x''를 ''n''만큼 이동시켜 암호화하는 함수 가 있을 때,[3] 복호화 함수 는 다음과 같다.[2]
:
(여기서 "mod"는 모듈로 연산을 의미한다. ''x''는 0부터 25 사이의 값을 가지며, A는 0, B는 1, ..., Z는 25로 표현된다. 만약 ''x'' - ''n''의 결과가 0보다 작으면 26을 더한다.)
4. 카이사르 암호 해독
카이사르 암호는 단일 치환 암호의 일종으로, 매우 간단한 방법으로 암호화되기 때문에 쉽게 해독될 수 있다. 해독 방법은 크게 무차별 대입 공격과 빈도 분석 두 가지로 나눌 수 있다.
- 무차별 대입 공격: 가능한 모든 시프트 값을 적용해 보는 방법이다. 영어의 경우 26가지의 시프트만 존재하므로, 모든 경우의 수를 대입하여 의미 있는 평문이 나오는지 확인하면 된다.[18]
- 빈도 분석: 암호문에 나타나는 문자의 빈도를 분석하여 해독하는 방법이다. 평문에 사용된 언어의 문자 빈도 분포와 암호문의 문자 빈도 분포를 비교한다. 예를 들어 영어의 경우 E, T 등의 문자는 자주 나타나고 Q, Z 등의 문자는 드물게 나타나는 특징을 이용한다.[21] 카이제곱 통계 등을 활용하여 빈도 분석 과정을 자동화할 수도 있다.[22][23]
카이사르 암호는 여러 번 암호화해도 보안성이 강화되지 않는다. 시프트 ''A''와 시프트 ''B''를 연속으로 적용하는 것은 시프트 (''A'' + ''B'')를 한 번 적용하는 것과 같기 때문이다. 수학적으로, 가능한 모든 키를 이용한 암호화 연산 집합은 함수 합성에 대해 군을 형성한다.[26]
4. 1. 전수 조사
카이사르 암호는 암호문 단독 시나리오에서도 쉽게 해독할 수 있다. 가능한 시프트 횟수가 제한적이기 때문이다(영어의 경우 26개). 공격자는 가능한 모든 시프트를 적용하여 메시지를 해독하는 무차별 대입 공격을 시도할 수 있다.[18]예를 들어, "exxegoexsrgi"라는 암호문에 대해 가능한 시프트를 적용하면 다음과 같다.
| 해독 시프트 | 후보 평문 |
|---|---|
| 0 | exxegoexsrgi |
| 1 | dwwdfndwrqfh |
| 2 | cvvcemcvqpeg |
| 3 | buubdlbupodf |
| 4 | attackatonce |
| 5 | zsszbjzsnmbd |
| 6 | yrryaiyrmlac |
| ... | |
| 23 | haahjrhavujl |
| 24 | gzzgiqgzutik |
| 25 | fyyfhpfytshj |
위 표에서 볼 수 있듯이, 시프트 4를 적용했을 때 "attackatonce"라는 의미 있는 평문을 얻을 수 있다.[18]
이처럼 가능한 모든 경우의 수를 대입하여 평문을 찾는 방법을 전수 조사라고 한다. 카이사르 암호는 시프트 가능한 경우의 수가 적기 때문에 전수 조사를 통해 쉽게 해독할 수 있다.
4. 2. 빈도 분석
카이사르 암호는 암호문에 나타나는 문자의 빈도를 분석하여 해독할 수 있다. 이를 빈도 분석이라고 한다. 평문에 사용된 언어의 문자 빈도 분포와 암호문의 문자 빈도 분포를 비교하는 방식이다. 예를 들어 영어의 경우, E, T 등의 문자는 자주 나타나고 Q, Z 등의 문자는 드물게 나타나는 특징이 있다.[21] 이러한 특징을 이용하여 암호문을 해독할 수 있다.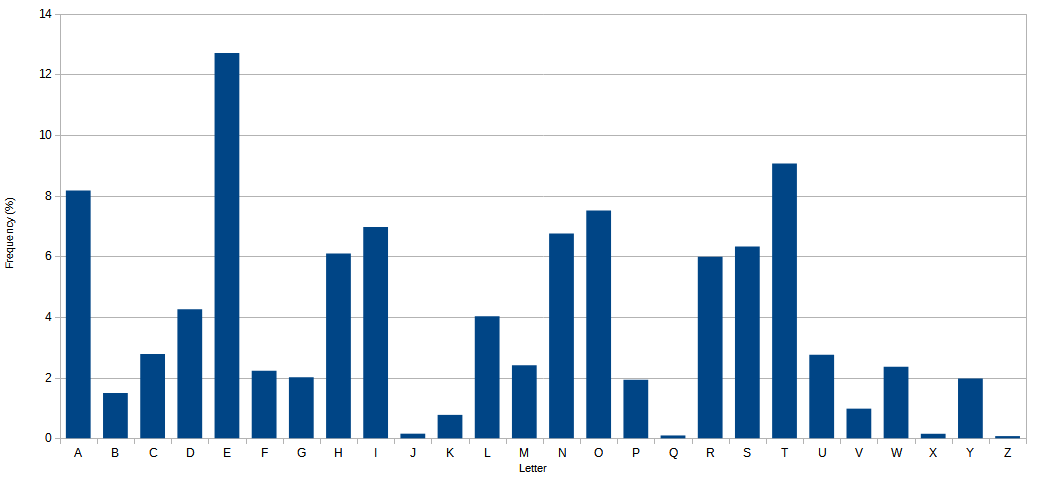
컴퓨터는 관찰된 빈도 분포와 예상 분포 간의 유사성을 평가하여 빈도 분석 과정을 자동화할 수 있다. 예를 들어, 카이제곱 통계를 활용하거나, 관찰된 언어 분포와 알려진 언어 분포 간의 제곱 오차의 합을 최소화함으로써 이를 달성할 수 있다.[22][23]
카이사르 암호의 유일성 거리는 약 2로, 평균적으로 키를 결정하려면 최소 2개의 암호문 문자가 필요하다는 것을 의미한다.[24]
4. 3. 기타 해독 기법
카이사르 암호는 암호문 단독 공격 시나리오에서도 쉽게 해독할 수 있다. 가능한 이동 횟수가 제한되어 있기 때문에(영어의 경우 26개), 공격자는 가능한 각 이동을 사용하여 메시지 또는 그 일부를 해독하는 무차별 대입 공격을 실행할 수 있다. 올바른 해독은 영어 텍스트로 의미가 있는 것이다.[18]또 다른 유형의 무차별 대입 공격은 암호문의 각 문자 아래에 알파벳을 해당 문자부터 시작하여 적는 것이다. 이 기술은 때때로 "평문 요소 완성"이라고 알려져 있다.[19][20]
다른 접근 방식은 문자 빈도 분포를 일치시키는 것이다. 암호문의 문자 빈도를 그래프로 표시하고, 평문의 원래 언어에서 해당 문자의 예상 분포를 알고 있으면, 그래프의 특정 기능의 변위를 살펴봄으로써 쉽게 시프트 값을 파악할 수 있다. 이것은 빈도 분석으로 알려져 있다. 예를 들어, 영어에서 문자 E, T (보통 가장 빈번하게 나타남) 및 Q, Z (일반적으로 가장 적게 나타남)의 평문 빈도는 특히 두드러진다.[21] 컴퓨터는 관찰된 빈도 분포와 예상 분포 간의 유사성을 평가하여 이 과정을 자동화할 수 있다. 예를 들어, 카이제곱 통계를 활용하거나, 관찰된 언어 분포와 알려진 언어 분포 간의 제곱 오차의 합을 최소화함으로써 이를 달성할 수 있다.[22][23]
5. 한계 및 취약점
카이사르 암호는 단일 치환 암호의 일종으로, 매우 쉽게 해독될 수 있어 오늘날에는 실질적인 보안 효과가 없다.[27]
카이사르 암호는 암호문 단독 공격에 취약하다. 공격자는 다음 두 가지 상황을 가정할 수 있다.
1. 어떤 단일 치환 암호가 사용되었는지는 알지만, 카이사르 암호인지는 모르는 경우
2. 카이사르 암호가 사용된 것은 알지만, 시프트 수를 모르는 경우
첫 번째 경우, 빈도 분석이나 단어 패턴 등 일반적인 단일 치환 암호 해독 기법을 사용할 수 있다.[47] 카이사르 암호는 알고리즘이 특징적이므로, 해독자는 규칙성을 파악하고 쉽게 해독할 수 있다.
두 번째 경우에는 무차별 대입 공격이 가능하다. 시프트 가능한 수는 영어 알파벳의 경우 26가지로 제한되어 있기 때문이다.[48] 예를 들어, 암호문의 일부를 시프트 가능한 수만큼 표로 작성하여 평문을 찾을 수 있다.[49][50]
암호문에 나타나는 문자의 빈도 그래프를 사용 언어의 일반적인 문자 빈도 분포와 비교하여 시프트 수를 추정할 수도 있다. 영어의 경우 'E', 'T'가 가장 많이 나타나고, 'Q', 'Z'가 가장 적게 나타나는 특징을 이용한다.[51] 카이제곱 검정 등을 통해 암호문과 평문의 출현 빈도를 비교할 수도 있다.[52]
자연어 평문의 경우 대부분 하나의 해독 결과만 나오지만, 평문이 매우 짧으면 여러 후보가 존재할 수 있다. 예를 들어 "MPQY"는 "aden" 또는 "know"로 해독될 수 있다.
카이사르 암호를 여러 번 적용해도 보안성은 향상되지 않는다. A만큼 시프트하고 B만큼 시프트하는 것은 (A + B)만큼 시프트하는 것과 같기 때문이다. 이는 수학적으로 군의 성질을 가진다.[53]
6. 활용 및 응용
카이사르 암호는 비제네르 암호와 ROT13 등의 부품으로 사용되기도 한다.[31] 그러나 카이사르 암호는 다른 단일 치환 암호와 마찬가지로 쉽게 해독되므로, 오늘날에는 유효하지 않다.[27]
카이사르 암호는 매우 단순하지만, 현대 암호의 중요한 요소인 규칙(알고리즘)과 키를 포함하고 있다.
- 규칙: 특정 문자를 사전순으로 정해진 숫자만큼 뒤(또는 앞)에 있는 문자로 바꾼다.
- 키: 사전순으로 이동할 문자 수. 카이사르가 사용한 암호의 키는 3이다.
6. 1. 비제네르 암호
비제네르 암호는 문장의 각 문자에 다른 시프트 수의 카이사르 암호를 사용하는 방식이다. 시프트 수는 암호 키의 단어를 반복하여 결정된다. 암호 키가 메시지와 동일한 길이의 임의의 문자열이고, 누구에게도 알려지지 않으며, 두 번 다시 사용되지 않는다면 그것은 일회용 패드가 되어 해독 불가능하게 된다.[43] 하지만 이러한 조건을 충족하는 것은 실제로는 매우 어렵다. 암호 키가 메시지보다 짧은 경우[43], 빈도 분석을 통계적으로 확장하여 암호문에 주기적인 패턴이 감지된다.[44]6. 2. ROT13
ROT13은 카이사르 암호의 일종으로, 알파벳을 13칸씩 이동하는 방식이다[31]。인터넷 게시판 등에서 내용을 가볍게 가리는 용도로 사용되기도 한다[31][40]。참조
[1]
웹사이트
Writing Secret Messages With a Caesar Cipher
https://golangprojec[...]
2021-11-30
[2]
간행물
Cryptology: From Caesar Ciphers to Public-Key Cryptosystems
1987-01
[3]
서적
Cryptology Unlocked
https://archive.org/[...]
Wiley
[4]
서적
Vita Divi Julii
http://thelatinlibra[...]
[5]
웹사이트
Cracking the Code
https://www.cia.gov/[...]
2017-02-21
[6]
서적
The Code Book
Anchor
[7]
간행물
Classical Cryptography
1962-12
[8]
서적
The Code Book
Anchor
[9]
서적
Jewish Traditions
Jewish Publication Society
2004
[10]
서적
The Name : a history of the dual-gendered Hebrew name for God
Wipf & Stock
2020
[11]
서적
The Codebreakers
[12]
서적
The Codebreakers
[13]
서적
Cryptology Unlocked
https://archive.org/[...]
Wiley
[14]
서적
The Codebreakers
[15]
서적
The Codebreakers
[16]
뉴스
Mafia boss undone by clumsy crypto
https://www.theregis[...]
2006-04-19
[17]
뉴스
BA jihadist relied on Jesus-era encryption
https://www.theregis[...]
2011-03-22
[18]
서적
Cryptology
Mathematical Association of America
[19]
간행물
Secret Communication among the Greeks and Romans
1969-04
[20]
서적
Elementary Cryptanalysis: A Mathematical Approach
Mathematical Association of America
[21]
서적
The Code Book
https://archive.org/[...]
Anchor
[22]
웹사이트
The Caesar Cipher
http://www.cs.trinco[...]
Trinity College
2002-07-15
[23]
웹사이트
Caesar Cipher Decryption
https://raw.org/tool[...]
2007-05-18
[24]
서적
Basic Methods of Cryptography
Cambridge University Press
1998-03-12
[25]
서적
Introduction to Cryptography with Maple
Springer Berlin Heidelberg
2012-12-19
[26]
서적
Cryptology Unlocked
https://archive.org/[...]
Wiley
[27]
웹사이트
substitution cipher
http://www.britannic[...]
Britannica.com
2015-12-17
[28]
간행물
暗号-歴史的観点から-
http://karn.lib.kago[...]
鹿児島工業高等専門学校
2011-02-23
[29]
웹사이트
White Paper : 簡単にわかる暗号の歴史
https://www.digicert[...]
デジサート・ジャパン合同会社
2021-05-16
[30]
간행물
暗号技術の動向
http://karn.lib.kago[...]
情報処理学会
2002-06-22
[31]
서적
Applied Cryptography
John Wiley & Sons
[32]
웹사이트
A Brief History of Cryptography
http://www.cypher.co[...]
Cypher Research Laboratories
2016-01-04
[33]
문서
古典ラテン語において、アルファベットの最後の文字はXであった。
[34]
간행물
Classical Cryptography
1962-12
[35]
서적
Fundamentals of Computer Security
Springer
[36]
서적
The Code Book
Anchor
[37]
웹사이트
Mezuzah and Astrology
http://www.chabad.or[...]
chabad.org
2008-06-13
[38]
서적
The Codebreakers
[39]
서적
The Codebreakers
[40]
서적
Cryptology Unlocked
Wiley
[41]
웹사이트
NetBSD 6.1.5 - man page for caesar (netbsd section 6)
http://www.unix.com/[...]
Unix and Linux Forums
2015-12-17
[42]
웹사이트
Man page of CAESAR
https://linuxjm.osdn[...]
JM Project
2015-12-17
[43]
문서
たとえば、[[南北戦争|アメリカ南北戦争]]において、[[アメリカ連合国|南部連合]]は「Complete Victory」といった、短いフレーズの暗号鍵を3つ使用していた。
[44]
서적
The Codebreakers
[45]
간행물
Cryptology: From Caesar Ciphers to Public-Key Cryptosystems
1987-01
[46]
서적
Cryptology Unlocked
Wiley
[47]
서적
Cryptology
Mathematical Association of America
[48]
서적
Cryptology
Mathematical Association of America
[49]
간행물
Secret Communication among the Greeks and Romans
1969-04
[50]
서적
Elementary Cryptanalysis: A Mathematical Approach
Mathematical Association of America
[51]
서적
The Code Book
Anchor
[52]
웹사이트
The Caesar Cipher
http://www.cs.trinco[...]
2002-07-15
[53]
서적
Cryptology Unlocked
Wiley
본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.
문의하기 : help@durumis.com